Detail of Publication
| Text Language | English |
|---|---|
| Authors | Kohei Miyamoto, Masakazu Iwamura and Koichi Kise |
| Title | A Quantum Algorithm for Finding k-Minima |
| Journal | Proc. 19th Asian Quantum Information Science Conference (AQIS2019) |
| Reviewed or not | Reviewed |
| Presentation type | Poster |
| Month & Year | August 2019 |
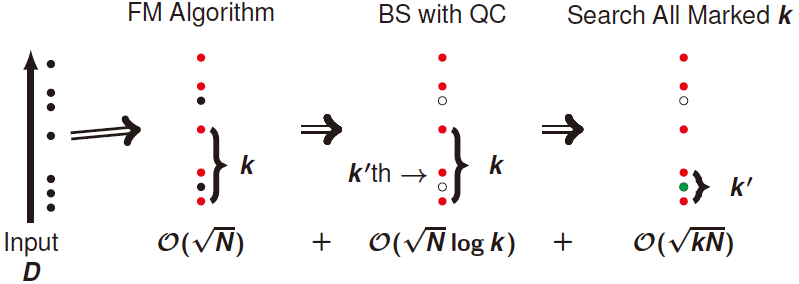
| Abstract | We propose a new \textit{finding $k$-minima} algorithm and prove that the query complexity is $\mathcal{O}(\sqrt{kN})$, where $N$ is the number of data indices. The primary difficulty of the problem is that it requires to return $k$ answers. For the problem, an extension of the Amplitude Amplification (we call it \textit{searching all marked $k$ indices} algorithm) finds all $k$ data with the query complexity of $\mathcal{O}(\sqrt{kN})$ if an appropriate threshold is given. We give a quantum algorithm that searches a good threshold with the complexity of $\mathcal{O}(\sqrt{N}\log{k})$. In addition, we briefly prove the query complexity of the \textit{searching all marked $k$-indices} algorithm, which is not well discussed so far. Our algorithm can be directly adapted to distance-related problems like $k$-Nearest Neighbor Search, clustering and classification. |
- Note
Full version of the paper is available at https://arxiv.org/abs/1907.03315 - Following files are available.
- Entry for BibTeX
@InProceedings{Miyamoto2019, author = {Kohei Miyamoto and Masakazu Iwamura and Koichi Kise}, title = {A Quantum Algorithm for Finding k-Minima}, booktitle = {Proc. 19th Asian Quantum Information Science Conference (AQIS2019)}, year = 2019, month = aug }